Complex Dynamical Systems, Nonequilibrium Statistical Physics, Many-Body Dynamics

Our research focuses on fundamental dynamical constraints that govern irreversibility, transport, and chaotic growth in nonequilibrium systems. We seek organizing principles, including geometric, inertial, and informational constraints, that determine what a system operating out of equilibrium can and cannot do.

Force Geometry and Irreversibility

A central direction of our current work is a geometric formulation of nonequilibrium irreversibility based on the instantaneous organization of forces. In driven overdamped systems, externally applied forces and information (entropic) forces associated with the evolving probability distribution are separated and compared through a time-dependent force-correlation measure. This captures how force misalignment produces irreversible dissipation.

Force geometry and irreversibility schematic

Figure 1: Irreversibility arising from the geometric relation between the externally imposed force and the information (entropic) force associated with the evolving distribution.

This framework provides an instantaneous characterization of dissipation without relying on steady-state or quasistatic assumptions. It distinguishes thermodynamic stall from true reversibility and identifies geometric waste: dissipation arising from force misalignment that cannot be removed by protocol optimization alone. Ongoing work extends this perspective to periodically driven systems relevant to optical-tweezer microrheology and soft matter, as well as to underdamped and higher-dimensional dynamics.

Speed Limits on Nonequilibrium Dynamics

We are developing a classical density theory that draws parallels with the density-matrix formulation of quantum mechanics. The theory is designed to ensure norm-preserving evolution in the tangent space of deterministic systems and applies to both Hamiltonian and dissipative dynamics.

Local perturbation growth rate schematic

Figure 2: How quickly can the growth rate of a local perturbation to a system change over time? [Das & Green, PRR (Letter), 2023]

One major finding is a set of model-independent dynamical speed limits for deterministic systems, closely analogous to quantum and stochastic speed limits. These results give time-information uncertainty relations for deterministic systems and bounds on the rates of entropy production and the variation of local stability indicators, including Lyapunov exponents.

Entropy production speed limit schematic

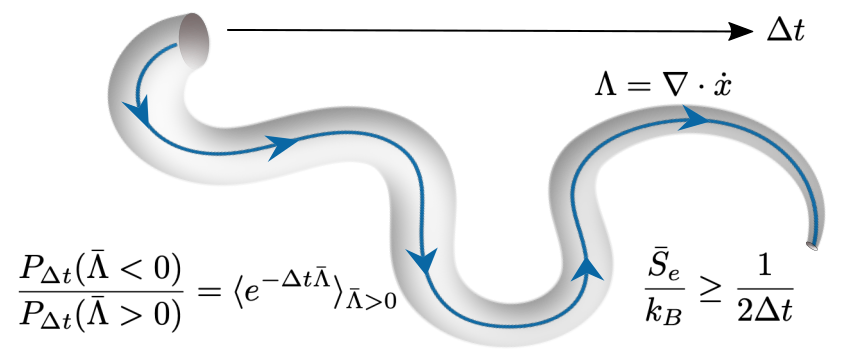
Figure 3: What is the minimum entropy production rate that can occur in a given time interval? [Das & Green, PRE (Letter), 2024]

An important element of this work is a classical Fisher information tailored to deterministic differentiable dynamics, analogous to quantum Fisher information. This measure connects phase-space geometry with dynamical instability. More broadly, the framework bridges the dynamical-systems perspective on stability and phase-space structure with the stochastic-thermodynamics perspective on entropy production and fluctuations.

Bounds on Chaos in Many-Body Systems

A major new direction is the development of intrinsic bounds on chaotic growth in classical many-body Hamiltonian systems. By analyzing the instantaneous stability matrix of Hamiltonian flows, we derive upper bounds on the largest Lyapunov exponent that apply at all times and cannot be transiently violated.

Dynamical speed limits schematic

Figure 4: Fundamental constraints on nonequilibrium dynamics, including an inertial ceiling and dynamical bounds on the rate of evolution.

These bounds separate geometry-blind contributions, controlled by local curvature, from geometry-aware contributions that retain spectral information and collective modes. In one-dimensional rotor chains, they predict forbidden regions in the Lyapunov exponent--energy plane. In the thermodynamic limit, the results reveal an inertial ceiling on chaotic growth in classical many-body systems.

Outlook

Our long-term goal is to develop a coherent and integrative framework for nonequilibrium dynamics that explains how irreversibility, chaos, and transport are shaped by geometric, inertial, and informational limits, rather than by detailed microscopic modeling alone.